MTS 2013 全國高中數學教學研討會
資訊融入教學組 差異化教學示例研發
99課綱高中數學第三冊第二章三角函數
台北市立建國高中 2013.1116
|
說明: |
||
資訊融入教學組 差異化教學示例研發
99課綱高中數學第三冊第二章三角函數
台北市立建國高中 2013.1116
|
說明: |
||
|
|
||
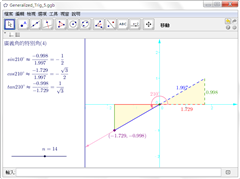 特別角的三角函數值(4) |
||
|
說明: |
說明: |
說明: |